跳到主要内容

安全多方计算

隐私问题是目前区块链技术所要解决的其中一重要问题，隐私保护不仅在区块链领域成为了重点研究内容之一，而且近几年不断出现的数据隐私泄露问题，也让公众对隐私保护有日益深入的认知。

Alaya 基于安全多方计算密码学算法实现一种隐私合约的解决方案，主要思想是将隐私计算算法通过合约进行发布，并由隐私保护需求的数据提供方和计算节点配合执行 MPC 协议，以实现数据的协同计算。

安全多方计算介绍#

安全多方计算，英文全称为 Secure Multi-Party Computation，简称 MPC。它指的是用户在无需进行数据归集的情况下，完成数据协同计算，同时保护数据所有方的原始数据隐私。具体来说，有$n$个计算参与方，分别持有私有数据$x_1,x_2,\dots ,x_n$，共同计算既定函数$f(x_1,\dots ,x_n)=y$。计算完成，得到正确计算结果$y$，且参与各方除了自己的输入数据和输出结果外，无法获知任何额外有效信息。

MPC 协议满足的基本性质是：

  • 输入隐私性： 协议执行过程中的中间数据不会泄露双方原始数据的相关信息；
  • 健壮性： 协议执行过程中，参与方不会输出不正确的结果。

构建通用 MPC 协议的典型范式之一是基于姚期智提出的针对两方计算的加密电路方法，并由 Beaver、Micali 和 Rogaway 进一步扩展到多方计算。目前 MPC 相关的协议或算法有 Garbled Circuit、Oblivious Transfer、Secret Sharing、BGW、GMW、BMR 等，同时工程实现上也有如SPDZ、LEGO、Sharemind、Fairplay 等不同的安全多方计算框架出来。典型的安全两方计算所使用的协议为加密电路（Garbled Circuit, GC）和不经意传输（Oblivious Transfer, OT）。

Garbled Circuit#

关于 Garbled Circuit 原理，可进一步参考此页面所做的解释。

目前已经有很多对加密电路进行优化的方案。包括 Free-XOR 技术，这意味着 XOR 门几乎无需加密，row reduction 和 half gate 技术，将每个 AND 门所需要的密文从 4 个降为 2 个。最近使用认证加密电路的研究结果实现了针对两方和多方恶意敌手模型下非常有效的协议。

若有兴趣对 Garbled Circuit 的理论知识作更深入的了解，可参考此论文。

Oblivious Transfer#

Oblivious Transfer，中文称为不经意传输，通常简写为 OT，它指的是发送者从一个值集合中向接收者发送单个值的问题，这里发送者无法知道发送的是哪一个值，而且接收者也不能获知除了接收值之外的其它任何值。形式化描述为：发送者有由$N$个值组成的集合，接收者有索引$i$（$0\leq i<N$）。协议执行完成，接收者只知道$N_i$，不知道$N_j$，这里$j\neq i$，并且发送者不知道$i$，这称为 1-out-of-N Oblivious Transfer。

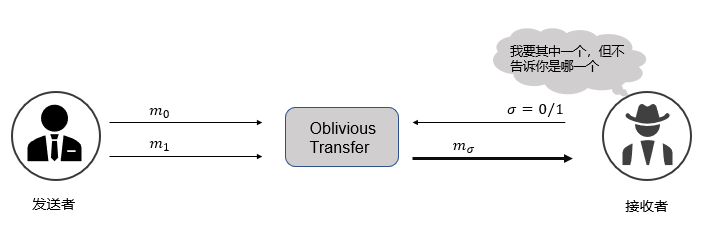
对于$N=2$，即为 1-out-of-2 Oblivious Transfer，接收者在计算加密电路之前，首先根据自己的输入数据获得与之对应的标签，由于标签是发送者定义的，因此接收者与发送者之间执行此 OT 协议。接收者按照其输入的每个比特，以$\sigma =0/1$为输入，发送者以标签$m_0$、$m_1$为输入。协议执行完成，接收者获得标签$m_\sigma$。图 7 为 1-out-of-2 OT 的示意图。协议执行的过程中，满足以下性质：

  • 发送者不可获知接收者选择的是哪个标签；
  • 接收者无法知道另一个标签$m_{1-\sigma}$。

图1: 1-out-of-2 OT示意图

两方安全计算的工作原理#

两方计算的实现过程为：

两个计算参与方 Alice 和 Bob，想共同计算$f(s,t)$，这里$s$为 Alice 所拥有的数据，$t$为 Bob 所拥有的数据，$f$为计算逻辑。首先，Alice 将$f$转换为相应的布尔电路$C$，其中$C$的每个门都有一个真值表表示门的输入输出。然后，Alice 对真值表进行加密处理，得到加密电路$\widetilde{C}$。同时，Alice 也对其输入进行加密，然后将加密后的输入与加密电路$\widetilde{C}$一同发送给 Bob。那么此时 Bob 就拥有了$\widetilde{C}$和 Alice 的加密输入（对应于 Alice 输入的标签），但却未被告知 Alice 的加密过程，因此 Bob 就无法获知该如何使用自己的输入。这时，Bob 通过与 Alice 之间执行 1-out-of-2 Oblivious Transfer 协议来获得加密输入（对应于自己输入的标签）。之后，Bob 使用两方的加密输入对加密电路逐个门进行解密，获得电路计算结果。

总体分为如下五个步骤，其详细过程解释如下：

1. 布尔电路生成#

假设$f(s,t)$是需要安全计算的函数，将此函数转换为布尔电路$C$，满足对任意$s,t$，有$f(s,t)=C(s,t)$。理论上任意函数均可表示成布尔电路。布尔电路的格式如图 1 所示：

图2: 函数转换为布尔电路

2. 加密电路生成#

Alice 将函数转换为布尔电路$C$后，将电路的每个门表示成如图 2 所示的真值表，接着通过加密这些真值表将$C$转化为加密电路$\widetilde{C}$。

图3: 将电路中的每个门表示成真值表

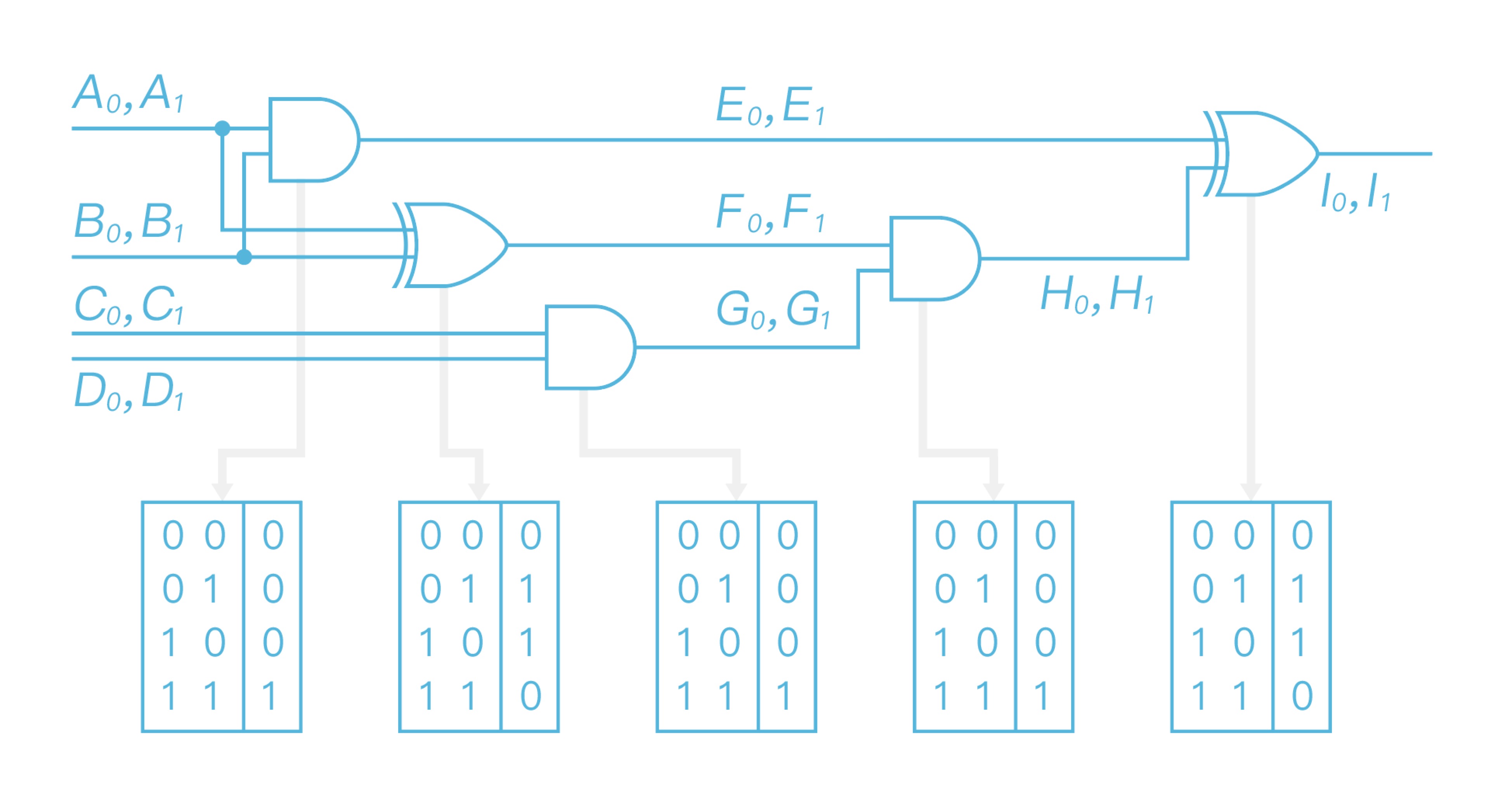
\ 接着 Alice 给电路中的每条线选取两个长度为$k$的随机数标签$A_0$、$A_1$（这里$k$为安全参数，通常为 128 bits）来代表 0、1。如$A_0$表示 0，$A_1$表示 1，对应关系只有 Alice 知道，依次逐个门进行替换，以图 3 第 1、2 两个 AND、XOR 门分别为例，其替换过程如图 4 所示：

图4: 标签替换真值表中的0/1

\ 所有门替换完成，生成如图 5 所示的表：

图5: 选取随机数替代每个门中的0/1

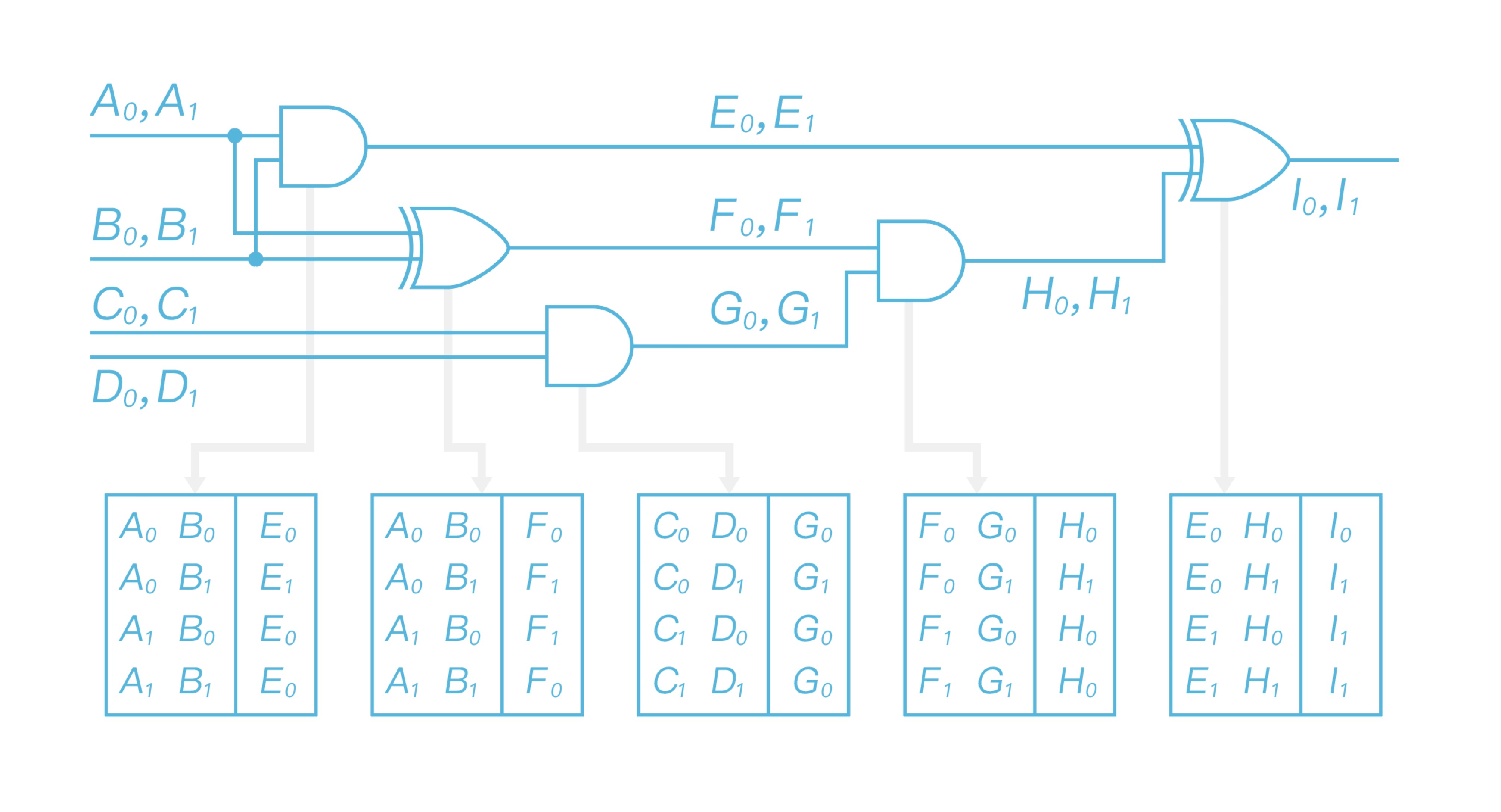
\ 然后 Alice 使用两个输入标签对每个门的输出标签进行加密，以第一个标签表的第一行为例，Alice 以两个输入标签$A_0$、$B_0$为输入进行双重 AES 加密输出标签$E_0$，得到$AES_{A_0}(AES_{B_0}(E_0))$，整个电路的所有其它电路门均以此形式进行处理，得到最终如图 6 所示的加密表，生成加密电路$\widetilde{C}$。可看出只有在获得输入标签的前提下，才能解密出加密表：

图6: 使用输入线标签加密输出线标签

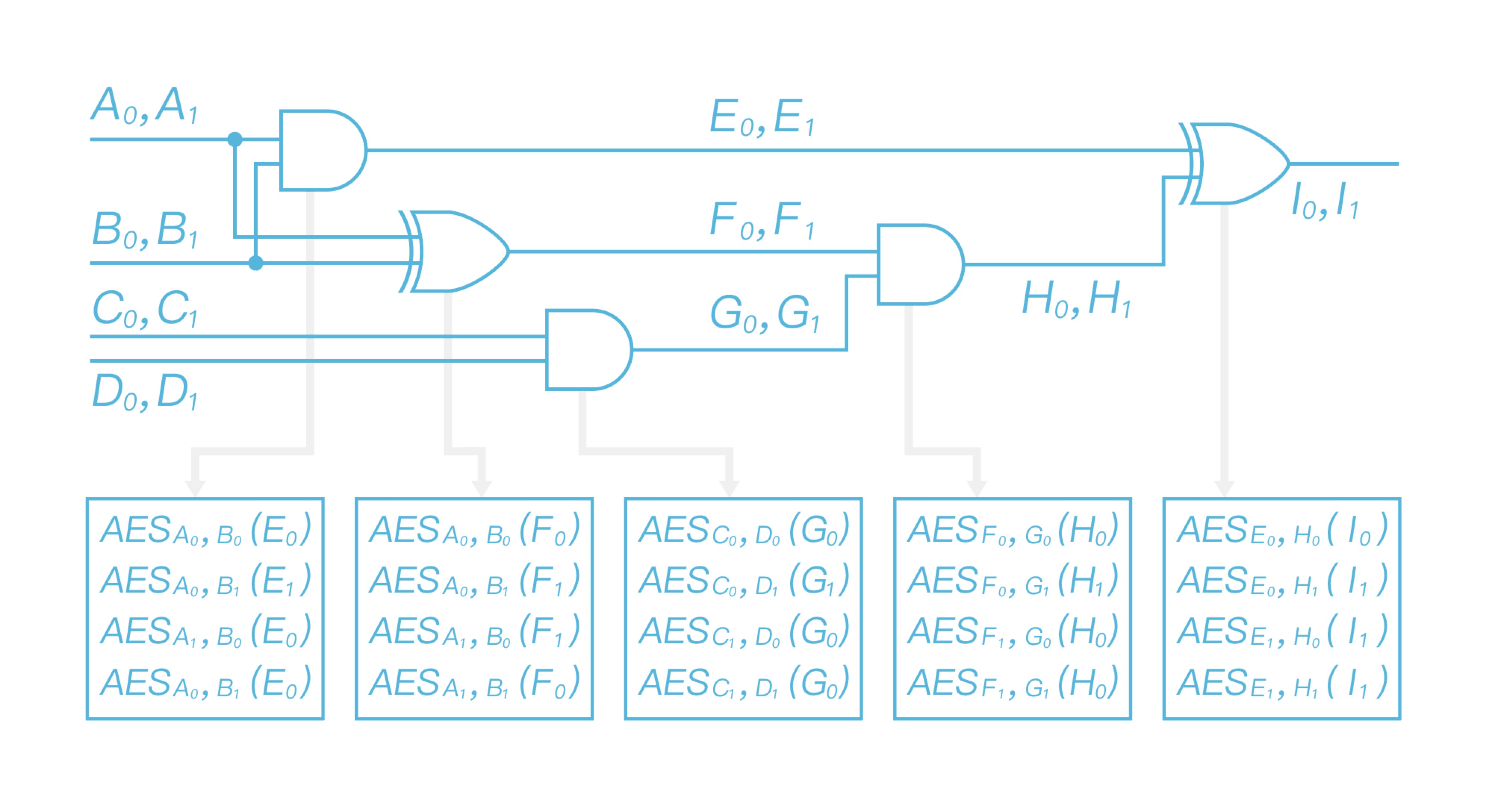
3. Alice 发送与自己输入相对应的标签#

生成加密电路后，Alice 也需要对其输入$s$进行加密。首先 Alice 将$s$转换为对应于电路$C$输入的布尔值，然后将布尔值的每一比特都用对应于$\widetilde{C}$输入的标签$A_0$、$A_1$等来替换，替换完成$s$的每一比特后，生成相应的标签。然后 Alice 将这些标签以及加密电路$\widetilde{C}$一同发送给 Bob。

假设 Alice 的输入为$s=s_0s_1=10$，则 Alice 根据其输入，发送给 Bob 的标签为$A_1$、$B_0$。

4. Bob 接收与其输入相对应的标签#

Bob 此时已有加密电路$\widetilde{C}$和 Alice 的标签，要想解密出加密电路，Bob 还需要对应于自己输入的标签来计算出加密电路。如前所述的加密过程，Alice 已经构造出 Bob 输入的标签，但却不知 Bob 的实际输入。Bob 知道自己的输入，但不能确定与其输入值相对应的标签。这里采用 1-out-of-2 Oblivious Transfer（见上文解释）来实现。对于 Bob 的每一个输入比特，他通过与 Alice 执行 Oblivious Transfer 来获得对应其输入的标签。这里，Alice 是发送者，Bob 是接收者，Alice 输入为标签，Bob 输入为 0 或 1，取决于实际的输入数据。这样 Bob 就可获得与自己输入所对应的标签，同时，Bob 无法获知关于电路任何其它有效的信息，Alice 也无从可知 Bob 实际的输入数据。

假设 Bob 的输入为$t=t_0t_1=01$，与 Alice 执行完 Oblivious Transfer 后，获得与其输入相对应的标签$C_0$、$D_1$，此时 Bob 就可完成对整个加密电路的解密。

5. 电路计算#

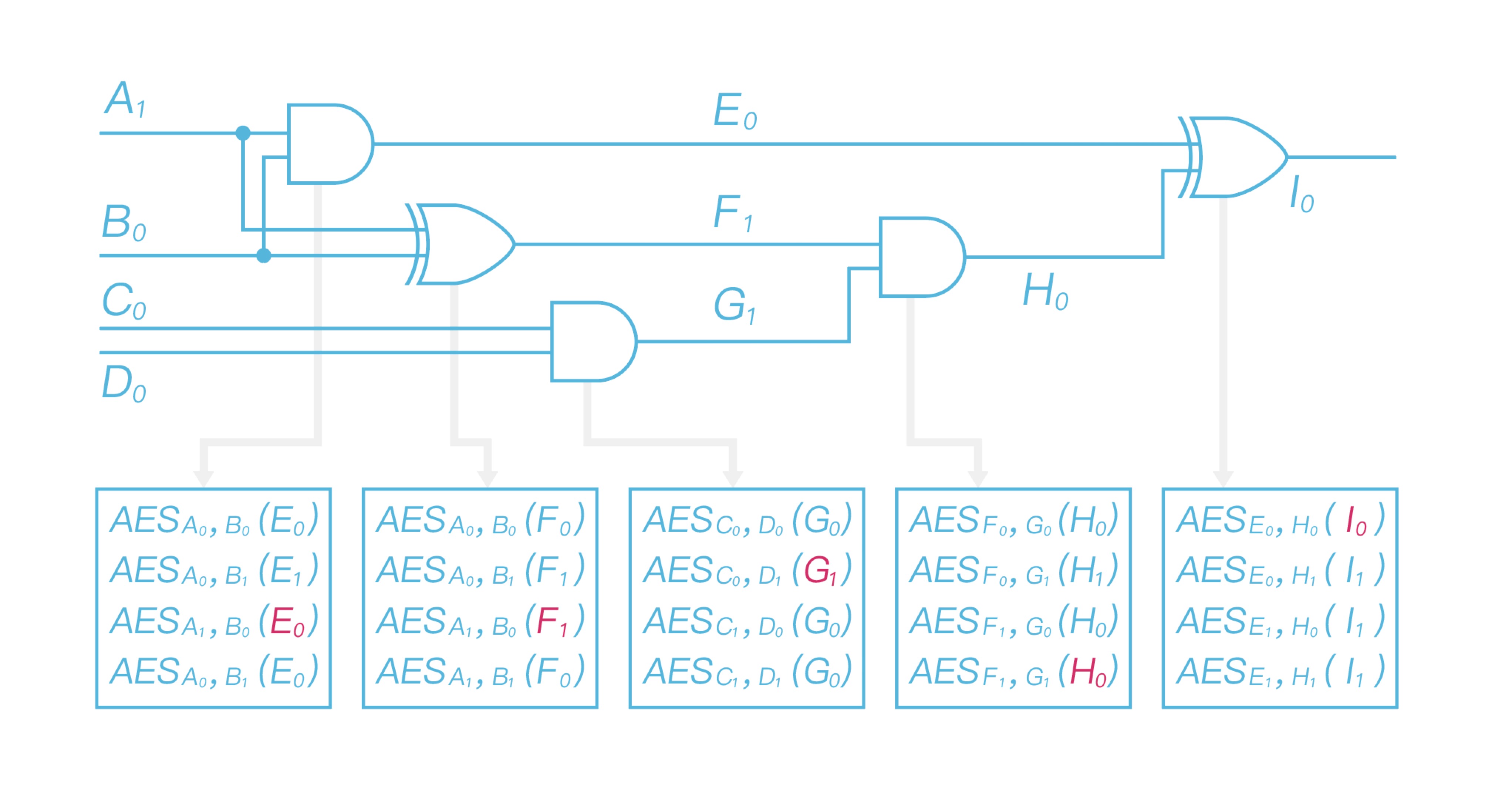
Bob 收到对应于自己输入的标签后，Bob 此时拥有的标签有$A_1$、$B_0$、$C_0$、$D_1$，然后逐个门依次进行解密，并将每个门解密后的输出值传递给下一个门，作为下一个门解密的输入。整个电路执行结束，Bob 获得输出标签，如图 7 所示。

对于第一个加密表，Bob 以$A_1$、$B_0$作为 key 输入，解密得到$E_0$；对于第二个加密表，以$A_1$、$B_0$作为 key 输入，解密得到$F_1$；对于第三个加密表，以$C_0$、$D_1$作为 key 输入，解密得到$G_1$；对于第四个加密表，以$F_1$、$G_1$作为 key 输入，解密得到$H_0$；最后以$E_0$、$H_0$作为 key 输入，解密最后一个加密表，得到最后的输出标签$I_0$。而标签的实际对应关系 Bob 知道，因此 Bob 可获得最终计算结果，并将结果发送给 Alice，这样双方获得计算输出结果。

图7: 按门依次解密获得输出标签

基本的两方安全计算模式#

图8：基本的两方安全计算实现模式

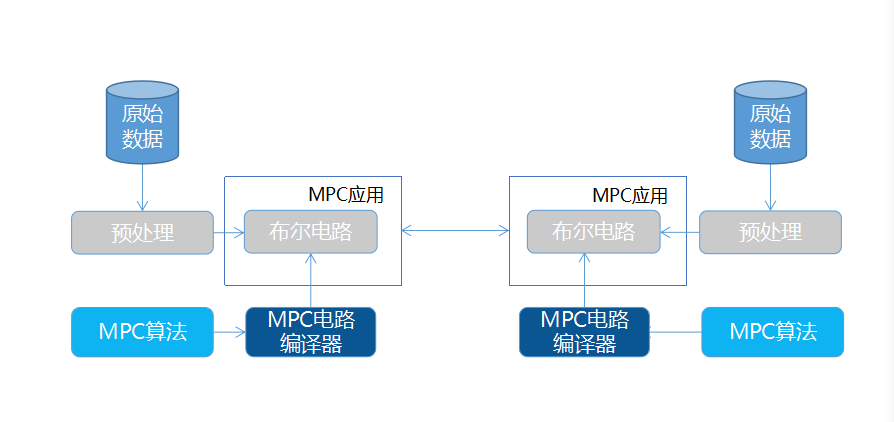
1、参与计算的其中一方编写业务算法，编写语言包括 C++、Java、Python 等高级编程语言(具体依赖于使用的多方全计算框架) 2、通过 MPC 编译器将业务算法编译成布尔电路（由 AND、XOR、NOT 门组成，常见格式为 Bristol）文件 2、参与计算的两方将各自拥有的原始数据进行预处理，转换为所编译布尔电路所需的输入数据格式 4、双方通过部署在各自本地的应用程序解释执行布尔电路，并相互通讯进行安全计算 5、计算完成，双方获得计算结果，并且通讯过程中的数据不会泄露双方原始数据的任何信息

Alaya 中的安全多方计算#

安全多方计算为 Alaya 实现隐私数据的协同计算提供了根本性的技术手段，在 Alaya 中结合 MPC 实现隐私合约，为具有多方参与数据作为输入的应用提供隐私保护，实现真正的隐私计算。

Alaya 的两方安全计算架构如下：

图9: Alaya的两方安全计算架构

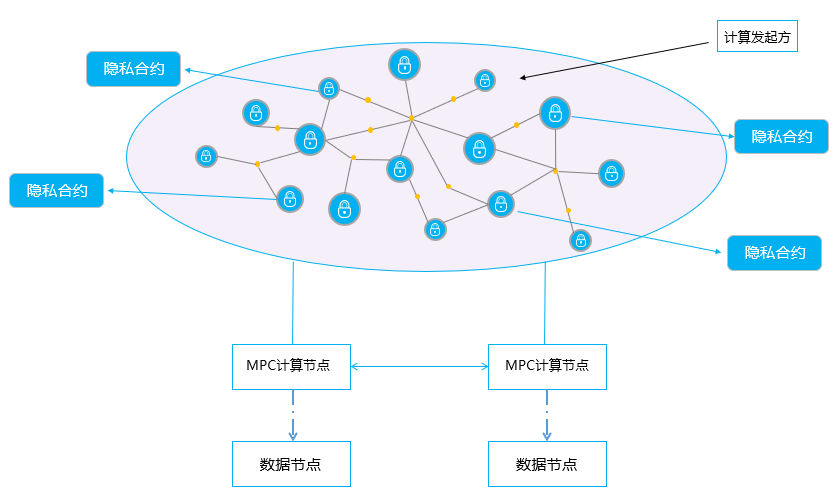
Alaya 的隐私合约同样支持高级语言编程，但不是编译成庞大的布尔电路文件，而是编译成更高效的 LLVM IR 字节码，并部署到 Alaya 网络上，在 MPC 计算节点内置的 MPC 虚拟机中以 JIT 方式执行。隐私合约的输入数据保存在数据节点本地，由数据节点在链下以安全多方计算方式进行隐私计算，并提交计算结果到链上。

Alaya 会持续优化当前已实现版本的 MPC 性能，并实现更先进的 MPC 协议，在以下几个方面进行改进：

  • 结合同态加密（HE）来降低 MPC 的通信复杂度
  • 从两方安全计算实现到三方以上的多方计算，以满足更加复杂多样化的应用场景